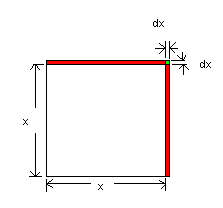
This is a square with area, a

Figure 1

a = x²

if we want to change the area, increase or decrease the area, with respect to the dimension x, then we want to know da/dx

We can show the graph of a(x) = x² as

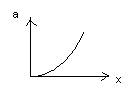
We know the change in area with repect to x is the slope of the curve x² .

da/dx, or a'(x) = 2x

To find the slope of a(x), we take the limit of (a(x + dx) - a(x))/dx as dx® 0.

a'(x) =( (x + dx)² - x²)/dx

a'(x) = (x² + 2xdx + dx² - x²)/dx

or

da/dx = ( 2xdx+ dx² )/dx

= 2x dx/dx + dx² /dx

= 2x

or

da = 2xdx

Looking at figure 1, we can see that the increase in area, da, with respect to a change in x, dx, is the shaded area or.

da = xdx + xdx + dx²

= 2xdx + dx²

da = 2xdx (we neglect the dx² term since it's very very small as dx® 0)

So.

a = x²

can also be expressed as

0 = a - x²

a is one way of expressing the area, and x² is another way of expressing the area.

a and x² are equal.

to find da/dx,

d(a)/dx - d(x²)/dx

d(a)/dx = da/dx

and

d(x²)/dx =( (x + dx)² - x²)/dx which leads to 2xdx/dx or 2x as shown above.